Simplifying Fractions Calculator

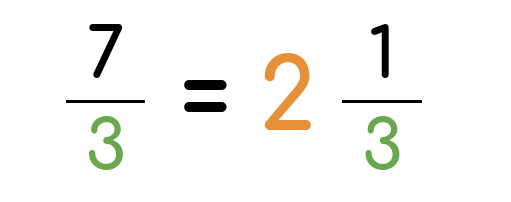
Fractions can be such a hassle to calculate. Simplifying or reducing fractions isn’t as easy as it may sound to many people.

This is when a simplifying fractions calculator comes in handy. It can save you a lot of time, and you can let your brain cells rest for a bit.

How Can Simplifying Complex Fractions Make Your Life Easier?

A fraction is basically a portion of a certain quantity taken from a whole. This can be any number, value, or even an item.

Whether you’re buying 1/2 a dozen of oranges or measuring 1/4 cup of sugar for a recipe you have in mind, these fractions are a crucial part of our everyday life. You use them without even realizing it.

However, some fractions can be a little more complicated than this. Therefore, they can take some time and effort to simplify.

A fraction simply consists of two numbers: a numerator and a denominator. We usually use whole numbers in the fractions to make it simple. We can also turn any decimal number into a fraction.

To reduce fractions, you need to find a common factor (GCF) that you can divide both numbers by. Ideally, you want to reach the simplest form possible of the fraction.

Using a simplifying fractions calculator can save you the hassle of this process, and it’ll help you do any calculation correctly.

What Is an Improper Fraction?

Improper fractions are simply when the numerator is bigger than or equal to the denominator. For example, 7/2 and 5/3 are improper fractions, while 1/4 and 1/2 are proper fractions.

What Is a Mixed Number?

A mixed number is a whole number like 1 or 2, with a proper fraction like 1/2 or 1/4. So, it’s basically a value between two whole numbers. For example, 1¼ is a mixed number.

What Is the Greatest Common Factor (GCF)?

The greatest common factor (GCF), also known as the highest common factor, of a set of values is the largest factor that all these values share.

For example, if the set of numbers was 12 and 16, we have 1, 2, and 4 as common factors for both of them. So, the greatest common factor is 4.

How to Simplify Improper Fractions to Mixed Numbers?

Improper fractions can sound a little complicated. However, once you turn them into mixed numbers, they’ll be easy to understand.

For example, 7/3 is an improper fraction. To simplify it, you need to divide the numerator by the denominator.

After that, we take the remainder and write it over the original denominator.

7/3 = 7 ÷ 3 = 2.3

So, 7/3 in mixed numbers will be 2⅓

How to Reduce Fractions?

You can reduce fractions by writing down the factors for both the numerator and the denominator. Then, determine the largest common factor.

After that, you can divide both numbers by the GCF and write down the simple fraction.

Other ways to simplify fractions

Reducing the numerator and denominator is not the only way to make numbers easier to understand. Depending on your needs, you may simplify a fraction by turning it into a decimal or a percentage value.

Converting fractions into decimal

This approach makes it easier to compare values. By turning a fraction into a decimal, anyone can instantly tell which value is greater.

Decimals make it also easier to add or subtract values. If you prefer to operate on decimals rather than fractions, use our fraction to decimal converter.

Converting fractions to percentages

Percentages, similar to decimals, make it easy to compare values and perform calculations.

However, percentages have an additional advantage over fractions and decimals. They are great for reports.

Use our fraction to percentage converter if you wish to convert any fraction into a percentage value.

Similar tools

Ratio to fraction calculator may be helpful if you need to convert ratio into a simple fraction.

Authors

Created by Lucas Krysiak on 2022-12-23 11:36:58 | Last review by Mike Kozminsky on 2024-04-10 12:31:43