Percentage calculator

Calcopolis provides you with a set of free online forms for solving real-life problems:

How to calculate X percent of Y?

For example, 5% of 200 is 10

How much percent of X is Y?

For instance: 20 is 40% of 50

How to calculate the percentage difference between X and Y?

For example, 12 is 20% bigger than 10

How do you determine the percentage change from X to Y?

e.g., 5 is a 25% increase from 4

How to calculate percentage increase/decrease?

For instance: 10 increased by 10% is 11

How to add or subtract a percentage?

For example, 20 minus 50% is 10

How to calculate the percent off?

Discount: 30% off $99,99 is $69.99

How to find your percentage test score?

The maximum number of points on the exam is 200. Your score is 150, which is 75%.

How to use our calculator?

Although the usage of the form above is simple, you should understand the concept of percentage to understand the equations. Otherwise, you could misinterpret the results. 

Of course, the examples above are intuitive and easy to understand, but real-life situations may not be as obvious. 

Not only could numbers be much bigger, but you might face more complex concepts like compounding percentages.

You may also be misled by similarly sounding terms but with entirely different meanings like percentage and percentage points. You may mix per mile with basis points and vice versa. 

So, percentages may be tricky, and even people with a solid math background may make mistakes from time to time. So let's start from the beginning. 

What is the percentage?

In short, one percent is a hundredth. Using percentages is a convenient method of expressing the relation of two numbers. Thanks two this, you can quickly compare large numbers and easily tell their differences.

The alternative methods of comparing numbers are ratios and fractions, but in most cases, percentages are more accessible and more natural for humans. That's why they are so commonly used. 

Percentages may be expressed in many forms:

• Using % sign: 5%
• As a decimal: 0.05
• As a fraction: 5/100

All the above examples represent the same value and can be used interchangeably, but it is a good practice not to mix them in one equation. 

What is the percentage point?

It is a straightforward but surprisingly often misunderstood concept. Many people treat it as a synonym for percent, but it represents an entirely different value.

One percent is one hundred, while one percent point is always 1 percent. Let's explain it by example.

Assume that your bank account pays you 1% of interest annually. If the bank increases the interest rate:

• By 1 percent - the interest rate will be 1,01% (1% of 1% is 0.01%)
• By one percentage point - the interest rate will be 2% (1% plus 1 percent point)

Can you see what a big mistake it can make when mixing both terms? A tiny modification of adding one extra percentage point essentially doubled the interest rate!

What's the percentage formula?

Since the one percent is just a ratio, the percentage equation can be expressed as follows:

result = number * percentage / 100

E.g.

What is 5% of 200

number * percentage / 100 = 200 * 5/100 = 10

If you wonder how to find the percentage of a number, then you have your answer.

How to calculate the percentage?

Below we are presenting some useful formulas for solving the most common problems. Examples and step-by-step explanations will follow each case to ensure everything will be well explained.

How do you work out percentages?

Solving percentage problems is easy. You just need to remember that percentage is nothing else like a fraction, i.e., 5% is the same as 5/100 or simply 0.05. So before we go any further, let's see the basics.

How to convert a percentage to a decimal?

Converting value to percentage is very easy - just divide it by 100 and remove % sign: 12.3% = 12.3/100 = 0.123

How to convert a decimal to a percentage?

The opposite situation of decimal to percent calculation is as easy as before. Just multiply the percentage by 100 and add the % sign: 

0.123 = 0.123 * 100% = 12.3%

Converting fraction to a percentage value

Converting ratios to percentages is also simple since the percentage is just another form of a fraction (with denominator 100). The only thing you need to do is convert the fraction to the common denominator.

For example:

⅘ = (4 * 20) / (5 * 20) = 80 / 100 = 80%

How do I calculate x percent of y?

Example: What is 10 percent of 50?

Formula: x% * y

Where: 

• x% percentage in our case 10%
• y initial number in our case, 50
•  
• 10% * 50 = 10/100 * 50 = (10 * 50) / 100 = 500 / 100 = 5
• So 10% of 50 equals 5 

How much percent of x is y?

The calculator uses the opposite approach to reverse the percentage, as explained below.

Example: What percent of 50 is 5

Formula: y/x = z%

Where:

• x initial number, we are referring to, in our case, 50
• y the value in our case 5
• z% - percentage value we are looking for  

5/50 = 10/100 = 10%

How do you find percentage change from x to y?

Example: What is the percentage change from 5 to 20?

Percentage Change Formula C = (y-x) / x * 100%

Where: 

• C - relative change 
• Y final value
• X initial value
•  

In this case:

C = (20 - 5) / 5 * 100% = 15/5 * 100% = 3* 100% = 300% 

How to find the percentage difference between two numbers?

Percentage Difference Formula: 

D = |X - Y| / ((X+Y) / 2) * 100%

Where:

• D - a relative difference
• |X - Y| absolute difference between given numbers

Example:

Example: What is the percentage difference between 200 and 50?

D = |200-50| / ((200+50) / 2) * 100% = 150 / (250/2) * 100% = 150 / 125 * 100% = 120%

Compounding percentages

This is a more complex situation. Imagine you want to increase some value each year by 10%

1000 +10% = 1100

1100 +10% = 1210

1210 +10% = 1331

1331 +10% = 1464

Notice that the value each year is increased by higher and higher numbers. The table above is equivalent to the formula:

1000 * 110% * 110% * 110% * 110% = 1464

This concept is also known as the compound interest formula and is most commonly used in finance. 

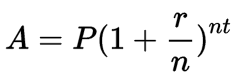
Where:

• A - final amount
• P - initial value
• r - interest rate
• n - number of times interest applied per period
• t - number of periods elapsed

You can find a more detailed explanation of this concept in our compound interest calculator.

Real-life applications

Store discounts: 30% off sale

You probably spot this a lot. This is the most common cause of percentage decrease calculation. 

$129,99 after 30% decrease equals 

$129,99 * (100% - 30%) = $129,99 * 70% = $90.99

Taxes

Taxes are most often in the form of percentages. For example, if you want to figure out the gross price for a given net price ($10) and sales tax value (20%), you can perform the following calculation:

GrossPrice = NetPrice * (100%+tax) = $10 * (100% + 20%) = $10 * 120% = $12

Helpful tools

Suppose you calculate the percentage value of money amount. You may need to adjust the amount to a more round and readable value. For a large number, you may find our rounding money calculator helpful. It allows you to round not only to the nearest dollar but to the nearest hundred or thousand.

Authors

Created by Lucas Krysiak on 2022-03-14 14:25:39 | Last review by Mike Kozminsky on 2022-03-30 14:45:20