Total return from regular saving of $0,00 monthly on 0.1% over 0.0252 months
| Initial amount: | $0,00 | |
| Monthly payment: | $0,00 | |
| Interest rate (nominal): | 0.1% | |
| Interest rate (effective): | 0.1% | ? |
| Time period: | 0.0252 months | |
| Amount paid: | $0,00 | |
| Interest before tax: | $0,00 | ? |
| Tax due: | $0,00 | ? |
| Future balance: | $0,00 | ? |
Regular monthly savings of $0,00 with annual interest rate of 0.1%, over 0.0252 months will give you total return of $0,00 and your future balance will reach $0,00.
| Initial amount | Interest ? | Tax ? | Final amount |
|---|
Impact of inflation
After 0.0252 months the purchasing power of $0,00 will be lower than today.
| Inflation rate | Future value in current money | Real return |
|---|---|---|
| 1% | $0,00 | $0,00 |
| 2% | $0,00 | $0,00 |
| 3% | $0,00 | $0,00 |
Compare your own scenario in our inflation calculator »
Did you know...
Each calculation on CalcoPolis has it's own url. You can:.
- bookmark it,
- include direct link on any website,
- sent it on email.
Consider alternative scenarios
Longer investment horizon
Monthly savings $0,00 with initial amount $0,00 with 0.1% interest rate.
| Sum of payments | Interests | Tax | Final amount | |
|---|---|---|---|---|
| 0 months | $0,00 | $0,00 | $0,00 | $0,00 |
Higher monthly savings
Same period of
0 months, interest rate 0.1%
and same initial amount of $0,00.
| Sum of payments | Interests | Tax | Final amount | |
|---|---|---|---|---|
| 0 | $0,00 | $0,00 | $0,00 | $0,00 |
Higher interest rate
Initial amount of $0,00 with monthly savings of $0,00 over 0 months
-
0.6% interest rate increase future balance to $0,00
-
1.1% interest rate increase future balance to $0,00
| Sum of payments | Interests | Tax | Final amount | |
|---|---|---|---|---|
| 0.1% | $0,00 | $0,00 | $0,00 | $0,00 |
| 0.6% | $0,00 | $0,00 | $0,00 | $0,00 |
| 1.1% | $0,00 | $0,00 | $0,00 | $0,00 |
Install CalcoPolis as App Add Calcopolis icon to homescreen and gain quick access to all calculators. Click here to see how »
Prepare your savings plan with the help of Calcopolis.
Table of Contents
- Functionality of this calculator
- How to calculate your savings growth?
- Formula 1. Compound interest for a single deposit
- Formula 2. Deposits at the end of each month
- Formula 3. Deposits at the beginning of each month
- Initial payment with series of regular deposits
- What is the best way to save money?
- Set your savings goal
- Saving Strategy
- How much should you save a month?
- Example 1. How to save 1 million dollars?
- Financial Independence, Retire Early (FIRE)
- Example 2. Saving 70% of a salary in order to achieve financial independence
- How many months’ salary should you save?

Functionality of this calculator
This tool will help you prepare your saving plan by giving you precise answers to the following questions.
How much money could I accumulate over time?
Calculate the future value of your savings after regular monthly payments with a fixed interest rate.
How long will it take to reach my financial goal?
Check how long it will take you to accumulate a specific amount of savings.
How much do I need to save per month to reach my goal?
Find out how much you need to save every month to reach your target value.
The calculator will provide you with an answer accompanied by colorful charts and detailed tables. Each simulation considers real-life scenarios, including the income tax you have to pay and the projected impact of inflation.
How to calculate your savings growth?
In order to find out the future value of your savings you need to use a formula for compound interest with regular monthly deposit. This is slightly more complex than the standard formula for a single deposit.
Formula 1. Compound interest for a single deposit
A = P(1+r/n)(nt)
Where:
-
A = the future value of the initial amount
-
P = the initial amount
-
r = the annual interest rate as a decimal number
-
n = the number of times that the interest is compounded per year
-
t = the number of years the money is invested for. (If you wish for a shorter period you can substitute 1/12 for one month)
Formula 2. Deposits at the end of each month
If you wish to add deposits at the end of each month you should pick the following formula:
A = PMT * (((1 + r/n)nt - 1) / (r/n))
Where:
-
PMT = the future value of the initial amount
Formula 3. Deposits at the beginning of each month
If you want to include regular payments at the beginning of each compounding period, you should use the formula below:
A = PMT * (((1 + r/n)nt - 1) / (r/n)) * (1 + r/n)
Since this is the most common case, this calculator adds deposits to the balance at the beginning of each month.
Initial payment with series of regular deposits
If you already have some savings and wish to start adding regular monthly deposits you can still use the formulas presented above. In order to do so, you need to split this into two scenarios and sum the results.
The procedure
-
Calculate the compound interest of the initial amount using Formula 1
-
Calculate the future value of regular deposits, using Formula 2 or 3
-
Sum the results
As you see, calculating the future value of your assets manually is a rather daunting and slow process. That’s why we created our online savings calculator to make this process as easy as possible.
What is the best way to save money?
It is not easy to give a single answer to this question, because each person is different and has their own goals, desires and prospects. In general, each saving plan depends on two main fundamentals:
-
your goal
The saving plan should be determined by your goal. If you collect funds for a down payment for the mortgage or save money for your retirement you should tune your strategy accordingly.
-
your psychology and risk tolerance
Each of us is not only different, but also at different points of life. Therefore the saving strategy will vary depending on how old you are and what your risk tolerance is.
Set your savings goal
Before you start saving it’s good to set your target. Saving just for its own sake will not help you stay motivated, which is a very important component of each successful plan. How can you expect to persevere in a resolution for many years and resist many temptations along the way if you lack motivation?
The most common reasons for saving are:
-
Buying a new car
-
Buying a new house
-
Wedding
-
Going on dream holidays
-
Your child’s higher education
-
Medical emergencies
-
Rainy-day fund
Pick one or a few of them, or even invent your own, but choose something. It will help to stick to the plan and keep focus.
Saving Strategy
This is a vast and complex topic. That’s why so many books are written about it. We will not try to summarize them here, but remember the most important piece of advice: any strategy is better than no strategy at all.
Without any consistent plan you will blunder your way from one idea to another , and you will keep changing your mind. It is the surest path to failure.
You may not only make many bad decisions, but also overpay the commission fees charged by your bank or a broker.
The most effective saving/investing ideas for beginners include passive investing, broad diversification and avoiding speculation.
How much should you save a month?
One may answer “as much as possible”, but in practice it looks good only on paper. If you are too hard on yourself you might lose perseverance and not reach your financial goal at all.
It’s better to be realistic, accumulate wealth a bit more slowly and get closer to your goal steadily, than to lose patience and enthusiasm.
Using our calculator you can find the sweet spot between fast capital accumulation and keeping a good living standard.
Please keep in mind that it is crucial to contribute at least 10% of your net earnings towards your savings reserve in order to make any difference in the future.
Example 1. How to save 1 million dollars?
A person who makes $4000 per month can reach $1,000,000 within 21 years when saving 30% of his salary per month ($1200) with an average annual interest rate of 10%.
Remember that an efficient saving strategy should not be limited to saving accounts and certificates of deposit. It may include a balanced portfolio of stocks, bonds, index funds, gold, etc.
Path from 0 to 1 million dollars in 21 years
https://calcopolis.com/saving/saving/a_0-i_1000-m_252-t_0-d_120000-c_monthly
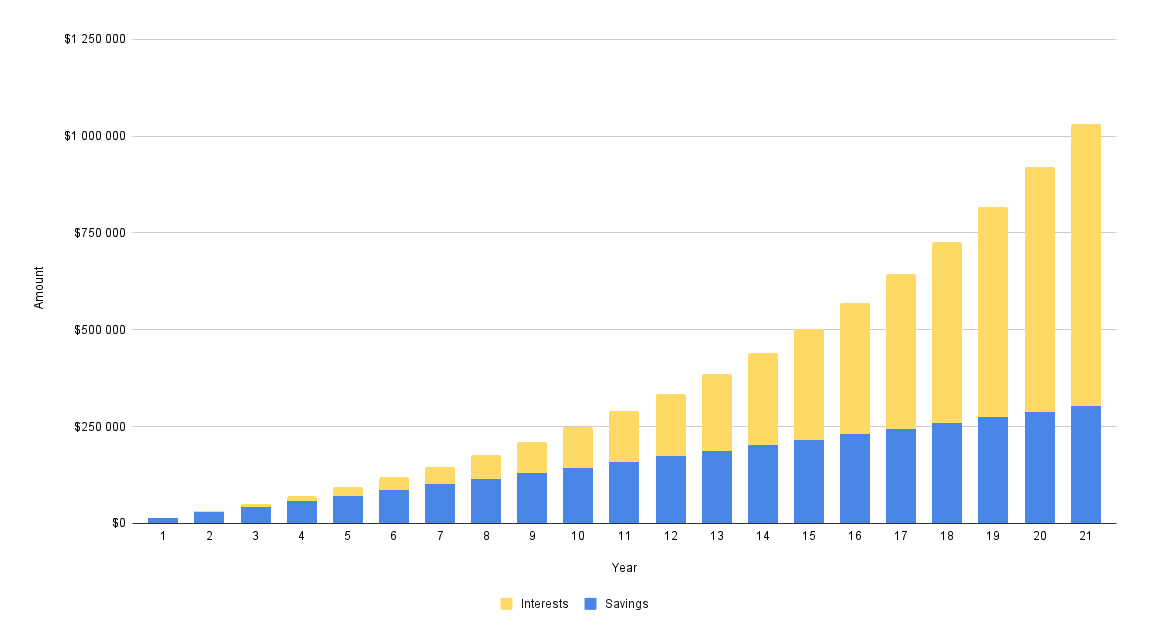
Key takeaways from this example
-
after 7 years monthly interests will exceed your monthly contributions
-
after 13 years total interests earned until that time will be higher than the sum of all previous contributions
-
after 21 years earned interests will be 2,4 times higher than the sum of all your contributions
-
at the end of the saving period you will exceed 1 million dollars net worth
Financial Independence, Retire Early (FIRE)
If you think that contributing 30% of your salary is tough and hardly anyone can afford it, you should get familiar with the FIRE movement.
FIRE is a philosophy for people devoted to reaching early retirement as soon as possible by implementing very rigorous saving regimes. Many followers of this methodology contribute 70% or even more of their salary to investments.
This way they can achieve financial independence and after a few tough years they can retire and not worry about money any more.
Example 2. Saving 70% of a salary in order to achieve financial independence
A person who makes $5000 per month can reach $1,000,000 within just 12 years and 3 months when saving 70% of his salary per month ($3500) with an average annual interest rate of 10%.
Path from 0 to 1 million dollars in 12 years and 3 months
https://calcopolis.com/saving/saving/a_0-c_1200-d_14700-i_1000-r_0-s_350000-t_0-m_14700
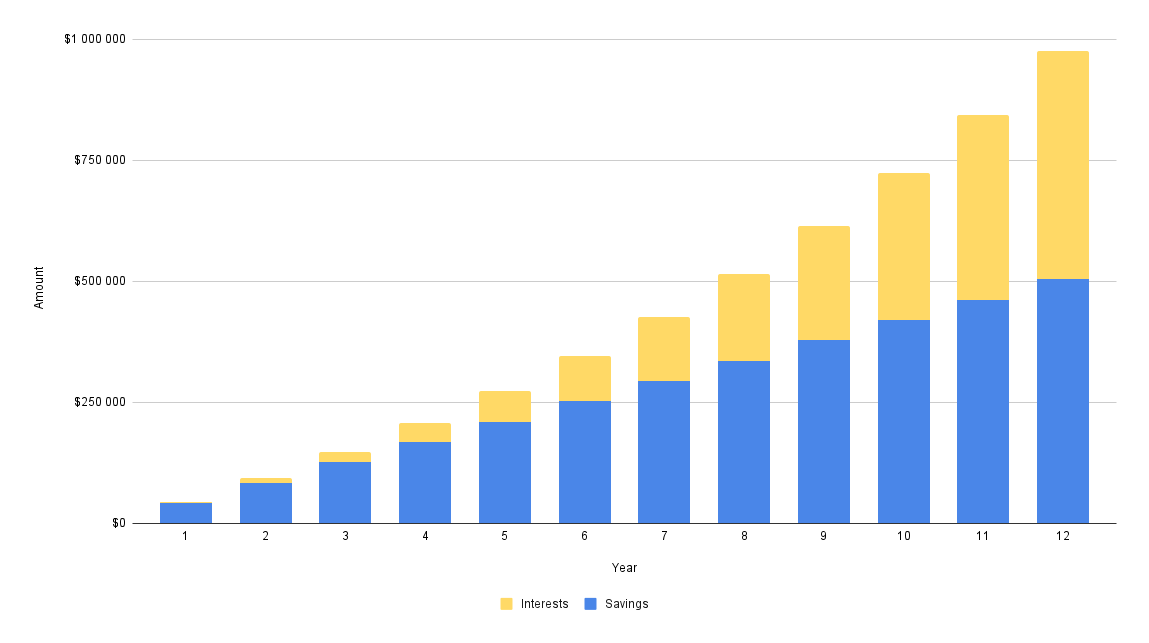
Note that this time the goal could be achieved nearly two times faster than before.
How many months’ salary should you save?
A rainy-day fund is very often the first step to financial independence and it’s sometimes called a little bit of freedom. If you can afford a few months without work, you don’t have to worry as much about losing your job and you could even try to start your own business.
This emergency fund could be the first step in building considerable wealth.
Authors
Created by Lucas Krysiak on 2022-02-24 14:58:20 | Last review by Mike Kozminsky on 2022-03-12 14:13:29

